DECAGON
ー注ー
動画は感覚的に解り易いのですが、本と同じく文字で読むことで、より頭に入ると思い解説を付けました。
任意の正方形ABCDを描きます。
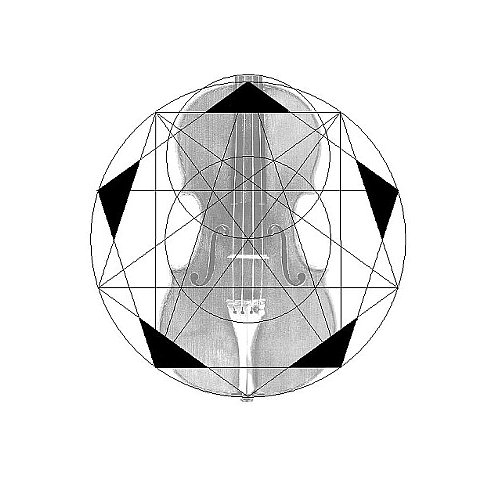
拙著『ヴァイオリンのf孔』より
1 正方形(縄と結び目によるの作図)
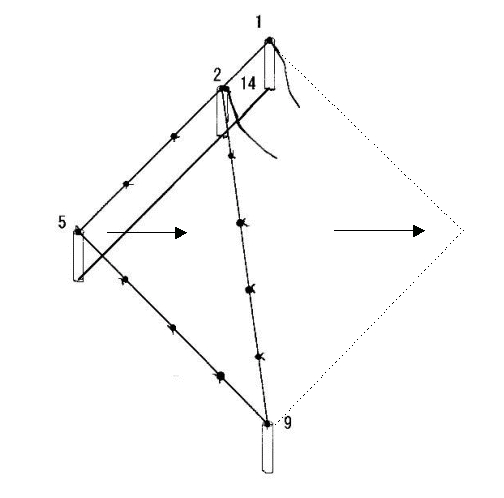
作りたい正方形の一辺となる長さ230m(例として、クフ王の第一ピラミッドで考える)に杭を打ち縄を張る。その縄をはずし、まず四つ折にして、その長さ57.5mの縄を15本結ぶ。第一、第五の結び目を先の一辺となる杭につけ、第十四の結び目を第二の結び目の所に杭で打ちつける。第九の結び目を引っ張っれば、直角が取れる。(3:4:5の直角三角形) 第五の結び目を杭から外し対角に引けば、求めたい正方形が求められる。 図1-1-1
.jpg)
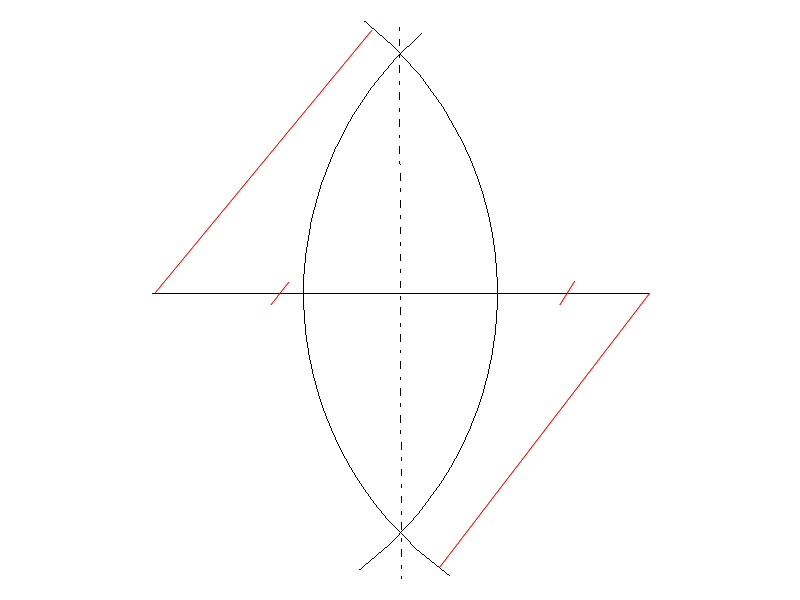
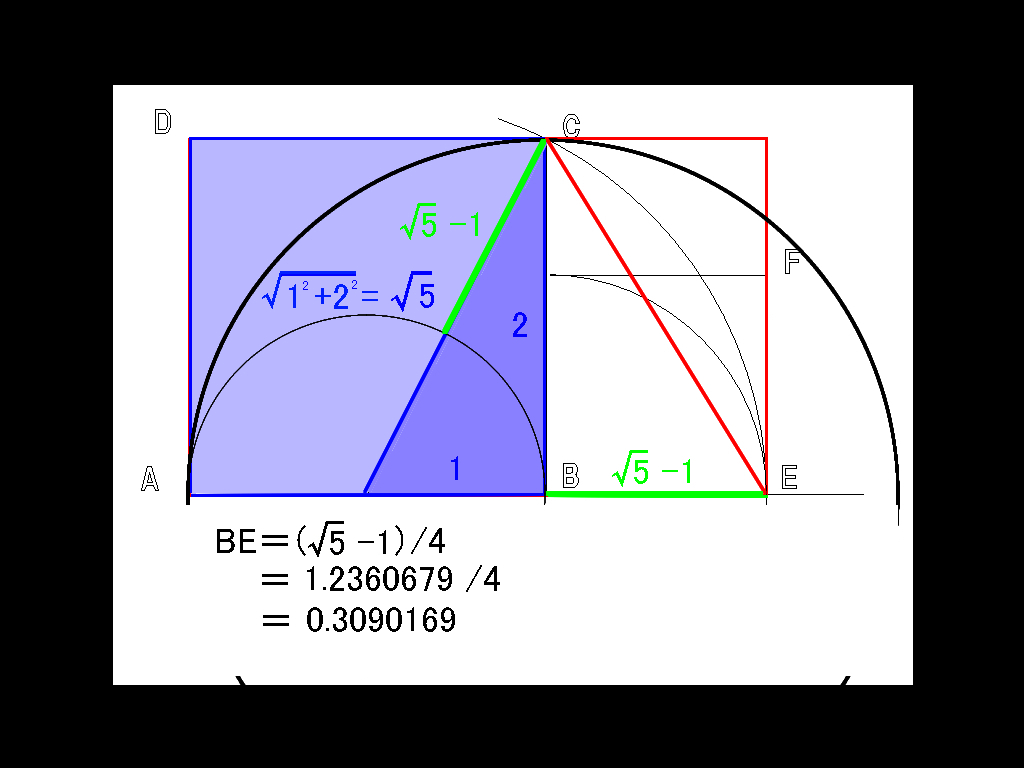
底辺ABの中点からCまでの長さを取ります。


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
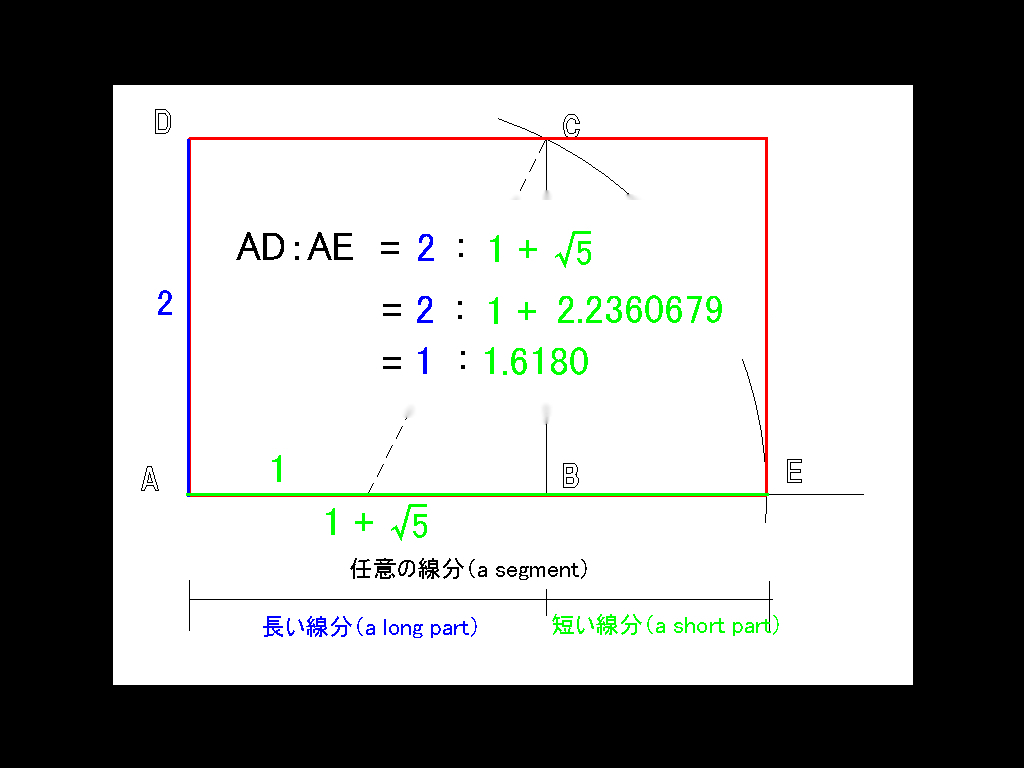
.jpg)
.jpg)
.jpg)
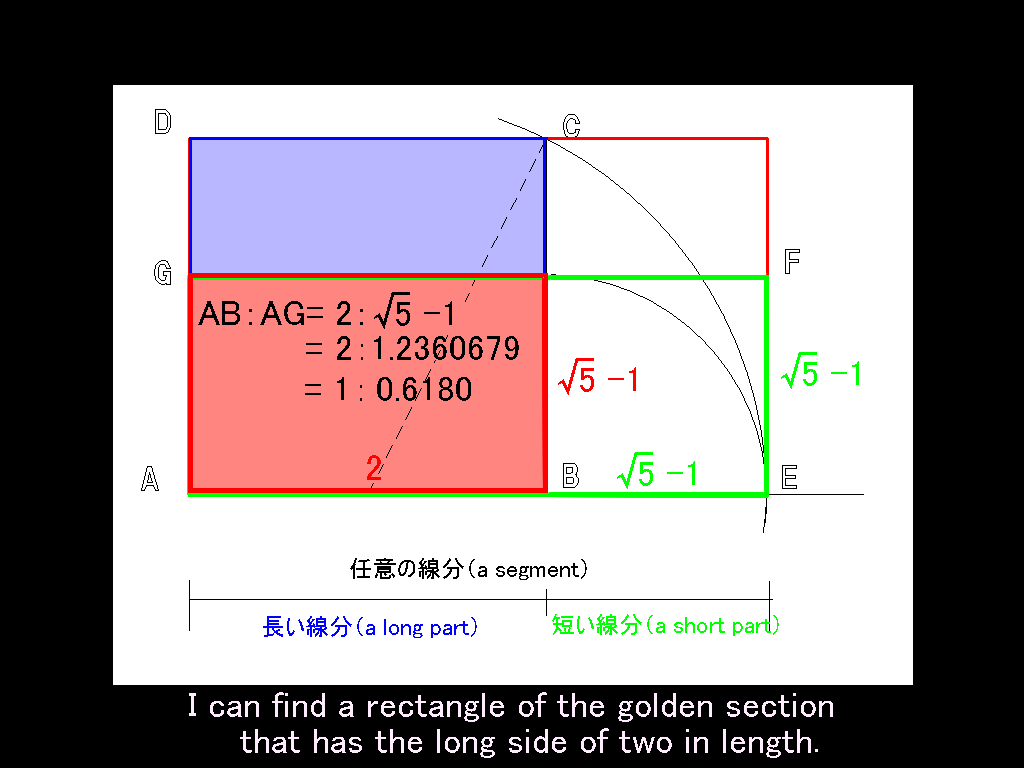
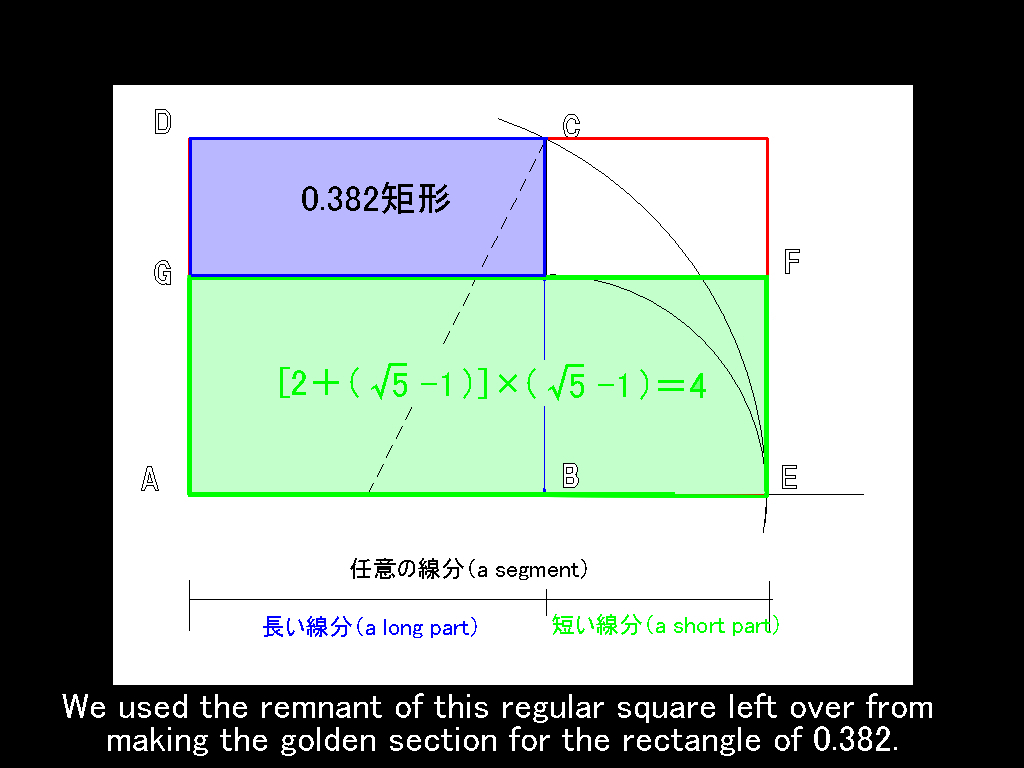

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
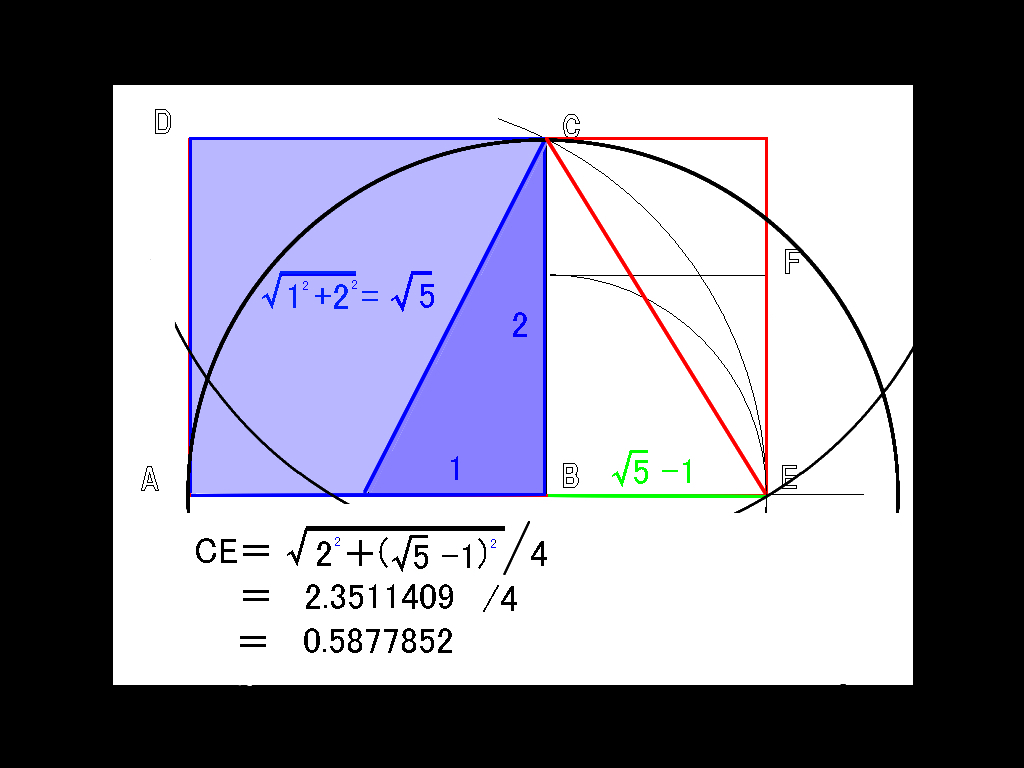
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)